Blättern

TEIL D

SYSTEMBESCHREIBUNG

Ich habe die Systembeschreibung des Synergetischen Modells in vier Bereiche aufgeteilt: Die geophysikalischen Koordinaten beschreiben die Position des Systems, welche für die Funktion maßgeblich ist. Unter den Maschinenelementen bildet der zentrale Rotationszylinder das wichtigste Element. Aus der anschließenden Beschreibung des Gesamtsystems erschließt sich dann die Struktur, und mit den Bewegungsstufen endlich auch die Funktion des neuen Energiewandlers.

1 - Geophysikalische Koordinaten

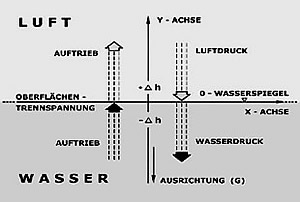
X - Achse:

Der natürliche Null-Wasserspiegel des Speisewasserreservoirs. Je nach Örtlichkeit ist es der Meeresspiegel, eine Fluß- oder Seeoberfläche oder auch der Wasserspiegel eines künstlich angelegten Reservoirs.

Er bildet die Grundlage aller Höhen- und Tiefenmaßstäbe des Energiesystems. (Etwa 5% der Gesamthöhe des Systems befinden sich unterhalb des Null-Niveaus, also im Bereich -D h.)

Y - Achse:

Die Ausrichtung entsprechend der Gravitation als Grundlage der lotrechten Aufstellung des Kernmaschinenelements.

2 - Maschinenelemente

Neben einer konventionellen hydroelektrischen Anlage befindet sich unter den Maschinenelementen des Synergetischen Modells ein Rotationskörper, der schon von seiner Größe her die dominierende Rolle spielt. Dieses Maschinenelement werde ich auch bevorzugt behandeln, da die übrigen Anlagenkomponenten (Turbinen, Generatoren usw.) allgemein gut genug bekannt sein dürften.

Der Rotationskörper wurde im Kleinformat bislang in den folgenden Grundformen ausprobiert:

A - Hohlzylinder
B - Sich nach oben hin verjüngender Hohlkegelstumpf
C - Sich nach unten hin verjüngender Hohlkegelstumpf

Das Funktionsprinzip des rotationsinduzierten Hochfließens bewies seine Wirksamkeit in allen drei Fällen. Welche Form sich bei Großanlagen als optimal herausstellen wird, kann ich nicht vorhersagen. Angeregt durch Prof. Rudolf Trostel von der TU Berlin nehme ich jedoch mit ziemlicher Sicherheit an, daß die Form die eines Zylinders sein wird, allerdings mit kelchförmigem Einfluß am unteren Ende. Auch intuitiv empfinde ich diese Form einer gedrungenen Röhre als ,richtig’ ⁽⁴⁰⁾. Eine gewisse Relevanz hat natürlich auch noch das Material dieses Maschinenelements - doch dies sei als Detail im Moment noch ausgeklammert.

Im Weiteren gehe ich bei dem Rotationskörper daher von der Form eines einfachen Hohlzylinders aus, der am unteren Boden einen strömungsunterstützenden Einfluß für das Speisewasser besitzt.

3 - Gesamtsystem

Die Energiestation befindet sich in unmittelbarer Nähe eines großen Wasserreservoirs (Meer, See, Fluß). Durch eine Zuführung unterhalb des Null-Wasserspiegels wird das Wasser unten in das Hauptmaschinenelement, den Rotationszylinder, hinein geleitet. Dieser steht aufrecht und ist auf einer schweren Schwungscheibe befestigt. Die Einheit aus Rotationskörper und Schwungscheibe wiederum ist auf einem Fundamentsockel frei gelagert.

Das unten zugeführte Wasser verläßt den Rotationskörper im Anschluß an seinen Aufstieg am oberen Ende, wo es in einem Umlaufkanal gesammelt und zum Turbinenschacht hingeleitet wird. Nach dem Fall fließt es dann wieder in das ursprüngliche Speisewasserreservoir zurück. Wir zapfen den erneuerbaren Speicher der Oberflächengewässer also nur sehr kurzzeitig an.

Innerhalb des Systems befindet sich demnach eine Wassermasse, die nach Beendigung der Startsequenz quantitativ immer gleich bleibt, qualitativ jedoch permanent wechselt. Ein ununterbrochener Wasserstrom durchfließt das Gesamtsystem hinauf und wieder hinab und erzeugt damit einen ebenfalls ununterbrochenen Stromfluß.

Neben den beschriebenen Maschinenelementen befinden sich in der Station noch die Antriebs- und Bremssysteme, sowie alle notwendigen Kontroll- und Regeleinrichtungen.

In der Grafik des Gesamtsystems sind alle Elemente und Untersysteme gekennzeichnet.

4 - Bewegungsstufen

Das eigentlich Neue des Synergetischen Modells ist das Kernelement, der Rotationszylinder. Allerdings nicht der ruhende - denn dieser wäre nicht viel besser als ein fast leerer Wassertank mit offenem Dach -, sondern der rotierende Zylinder!

Nach dem Start der Rotation ist seine Funktion zu Beginn rein rezeptiv. Im Leerlauf - d.h. bei unterbrochenem Wasserzufluß - würde diese Rezeptivität aus dem ausschließlichen Speichern mechanischer Energie in Zylinder und Schwungscheibe bestehen. Ist der Wasserzufluß jedoch offen, sieht die Sache schon etwas anders aus.

Der Rotationskörper wird solange beschleunigt, bis die vorab gewählte Drehzahl erreicht ist. Da die Rotation um die lotrechte Achse stattfindet, ist die Reibung minimal. Die hierdurch entstehenden Verluste konnten mangels Versuchsanlagen noch nicht näher untersucht werden, ich denke jedoch nicht, daß es sich dabei um relevante Verluste handeln wird. Auch hierfür gibt es gute Gründe, auf die ich noch zu sprechen komme.

In einem System effizienter Größe wird auch der Rotationskörper recht groß sein. Vielleicht mit einer Höhe von 100 m und einem Durchmesser von 30 m, wenn der Rotationskörper inklusive Schwungscheibe runde 1.000 t wiegt? Oder ist das zu groß? Es gibt auch andere Meinungen, die davon ausgehen, daß die Mindestgröße des Zylinders 50 m betragen müßte, damit die postulierten Effekte auch tatsächlich wirksam werden können (Stichwort: Schwellenwert). Darüber mehr in der physikalischen Analyse von Harald Kautz-Vella (pdf-Datei).

Die Drehzahl wird nicht besonders hoch ausfallen, da sie ausschließlich vom Verhältnis der Höhe zum Durchmesser abhängt. Bei den bisherigen Kleinstmodellen hat sie zwischen 5 und 10 Umdrehungen pro Sekunde betragen, und ich nehme an, daß es sich auch bei größeren Anlagen so verhalten wird. Es kommt schließlich darauf an, viel Wasser nach oben fließen zu lassen, und nicht wie schnell. Daher sollte die Rotationsgeschwindigkeit stets so niedrig wie möglich angesetzt werden.

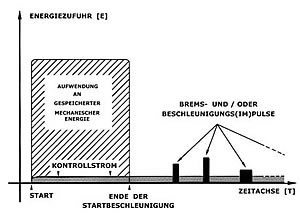
Energiezufuhr

Wegen des hohen Gewichts müssen zwar einige Millionen Dyn oder Erg aufgewendet werden, um diese gewünschte Drehzahl zu erreichen ⁽⁴¹⁾. Die hierbei investierte Energie ist aber nicht als Verlust zu betrachten, sondern als andauernd gespeicherte Bewegungsenergie, die den Wasserhochfluß überhaupt erst in Gang setzt.

Die Gesamtkapazität des Systems steigt mit der Kapazität zur Speicherung mechanischer Energie, welche ihrerseits mit steigendem Gewicht ebenfalls steigt. Ob diese Startenergie dabei mittels Sonnenkollektoren, Windenergie, Akkumulatoren oder durch das öffentliche Stromnetz aufgebracht wird, ist im Prinzip ein unwesentliches Detail.

Nach dem Erreichen der erforderlichen Drehzahl soll die gleichbleibende Rotation aufrechterhalten werden. Da eine weitere Beschleunigung nicht mehr erforderlich ist, wird ab diesem Stadium nur noch soviel Energie aufgewendet wie notwendig ist, um dem Rotationskörper seine gleichbleibende Geschwindigkeit zu erhalten. Diese Arbeit kann ein automatisches Kontroll- und Regelsystem übernehmen, das je nach Bedarf entweder Brems- oder Beschleunigungsimpulse abgibt. In der nebenstehenden Abbildung habe ich diese exogene Energiezufuhr für Start, Kontrolle und Regelung der Drehzahl dargestellt. Ich betone nochmals: Es ist nicht notwendig, stetig weiter zu beschleunigen!

Durch diese Anordnung funktioniert das Gerät auf Dauer. Es ist damit jedoch keineswegs ein Perpetuum Mobile - es sei denn, wir folgen der Betrachtung, daß der gesamte Kosmos ein dauerhaftes und ewiges Perpetuum Mobile ist. Denn hier wie dort wird Energie weder erschaffen noch vernichtet, sondern stets nur umgewandelt. Aber dies dafür immer, stetig und in allen nur denkbaren Formen. Zum Thema Dauer sagte Lama Anagarika Govinda einmal:

„Dauer ist ein Zustand, dessen Bewegung nicht durch Hindernisse erschöpft wird. Es ist nicht ein Zustand der Ruhe (im Sinne der Bewegungslosigkeit), denn bloßer Stillstand ist Rückschritt. Dauer ist somit eine sich selbst erneuernde Bewegung eines organisierten integrierten Ganzen, die in Übereinstimmung mit unveränderlichen Gesetzen vor sich geht.“ ⁽⁴²⁾

In meinen Augen kann man dies auch sehr gut aus einem technischen Blickwinkel verstehen: Diese ,sich selbst erneuernde Bewegung’ wird im vorliegenden Fall durch die integrierten Regelsysteme realisiert, welche aufgrund von Kontrollmessungen und Rückmeldungen bedarfsspezifische Brems- oder Beschleunigungsimpulse auslösen - im Rahmen bestimmter Grenzwerte und mit möglichst kleinen Schwankungen. Hierdurch wird dann jene Übereinstimmung mit ,unveränderlichen Gesetzen’ erreicht - sprich mit der vorprogrammierten Geschwindigkeit.

Und wenn wir dann nicht den Fehler machen, Ruhe mit Bewegungslosigkeit gleichzusetzen, könnten wir auch treffend sagen: "In der Ruhe steckt die Kraft!"

Es mag an dieser Stelle vielleicht ganz nützlich sein, an die Spekulationen zu erinnern, die sich um den grundlegenden Unterschied zwischen der gradlinigen und der kreisförmigen Bewegung drehten (Aristoteles, Kopernikus, Galilei, u.a.). Von Kopernikus stammt die Aussage, daß ein "einfacher Körper eine einfache Bewegung hat, was sich hauptsächlich im Fall der Kreisbewegung zeigt, solange sich der einfache Körper an seinem natürlichen Ort befindet und seine Einheit behält. An diesem Ort kann die Bewegung nur kreisförmig sein, sie bleibt völlig in sich geschlossen, als ob der Körper ruhe" ⁽⁴³⁾. Und Newton erklärt in seinem 1. Axiom (von 1687): "Jedes Objekt beharrt in demselben Zustand gleichmäßiger Bewegung, solange nicht eine Kraft auf es wirkt" ⁽⁴⁴⁾.

Übertragen wir diese Aussagen versuchshalber einmal auf das Synergetische Modell:

Für unser Rotationsmaschinenelement bildet die Drehung den ,Zustand’, in dem es beharren soll. Wir können das Erreichen dieses Zustandes durch Zu- oder Abführen von Energie oder Masse ermöglichen, und ebenso können wir dadurch auch dafür sorgen, daß dieser Zustand erhalten bleibt. Als Maß für den Widerstand eines rotierenden Körpers gegen die Änderung der Rotationsgeschwindigkeit gilt das ,Trägheitsmoment’, das mit der Masse und dem Quadrat des Halbmessers zunimmt, und das die Erhaltung des erreichten Zustands entgegen äußeren Widerständen mit unterstützt.

Um den Körper in seiner Drehung beharren zu lassen, ist weitaus weniger Energie erforderlich, als notwendig ist, ihn aus dem Stand heraus zu beschleunigen. Die Schwungscheibe am unteren Ende des Rotationskörpers dient - neben ihrer Hauptaufgabe zur Kapazitätssteigerung des Gesamtsystems - auch der Steigerung des Trägheitsmoments, der Stabilisierung der Rotation und der kurzzeitigen Überbrückung etwaiger Ausfälle im Kontroll- und Regelsystem. Völlig reibungsfreie Lagerungen - wie z.B. supraleitende Magnetlager - zu installieren, ist sehr aufwendig und meines Erachtens nicht notwendig. Zur Stabilisierung einer dauerhaften wechselwirkenden Rotation ist sogar eher Bremsenergie erforderlich als weitere Antriebsenergie - zumindest laut den Angaben des Innovators, der den Einbau eines entsprechenden Bremssystems unbedingt anempfiehlt!

Auch die Rotationsrichtung spielt im Gesamtverhalten eine Rolle. Durch den Einfluß der Erdrotation wirkt eine Corioliskraft auf das sich drehende Maschinenelement. Wenn sich herausstellt, daß die optimale Drehrichtung des Systems analog der atmosphärischen Strömungen ist, dann müßte sich das Maschinenelement auf der Nordhalbkugel der Erde im Uhrzeigersinn und auf der Südhalbkugel im Gegensinn drehen - oder vielleicht genau umgekehrt? Wirklich feststellen läßt sich dies wohl erst anhand von Versuchsanlagen an unterschiedlichen Standorten. Ich werde im Kapitel ,der Planet’ darauf noch zurückkommen.

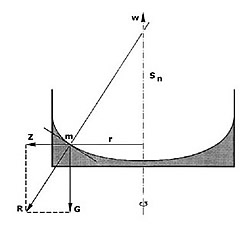
Rotierende Schale

Die erste der Bewegungsstufen erleben wir in der Phase des startenden Rotationskörpers, in welchen das Wasser hineindringt, und der dadurch ein anderes Verhalten zeigt, als ein Rotationskörper im Leer- bzw. Trockenlauf. Beginnen wir daher mit der folgenden Betrachtung: Rotiert eine Flüssigkeit in einem Zylinder, so wirken auf die Masseteilchen (m) zwei Kräfte ein, nämlich das Gewicht [G = m · g] und die Fliehkraft [Z = m · r · w²], wobei (w) die Winkelgeschwindigkeit der Rotation bedeutet. Beide Kräfte vereinigen sich zu der Resultante (R), die senkrecht zur Flüssigkeitsoberfläche steht, so daß (S_n) als Subnormale, in Projektion der Verlängerung von (mR) bis zur Achse, auftritt.

Bei gleichbleibender Winkelgeschwindigkeit (w) ist demnach die Subnormale konstant, der Achsenschnitt der Rotationsfläche eine Parabel, und die Fläche selbst ein Rotationsparaboloid.

Infolge der Trägheit haben alle Masseteilchen eines sich drehenden Körpers das Bestreben, in ihrer zur Drehungsachse senkrechten Drehungsebene zu bleiben - und der sich drehende Körper behält, sich selbst überlassen, seine Drehachse auch unverändert bei. Die Parabel, aus der durch Rotation der Paraboloid entsteht, gilt in der analytischen Geometrie als symmetrische und ins Unendliche verlaufende Kurve. In unserem Beispiel entsteht der Paraboloid durch die Rotation der Flüssigkeit in einem rotierenden Zylinder. Denn würde sich der Zylinder selbst nicht auch drehen, dann würden Wandreibung und Scherkräfte die Rotation stark abbremsen und der Paraboloid schnell verflachen.

Eine interessante und seltene Ausnahme bildet hierzu nur Helium II, das bei 2,2° über dem absoluten Nullpunkt (0°K = -273,17°C) ein recht seltsames Verhalten zeigt, während es bei normaler Raumtemperatur auch ,normal’ gasförmig ist. Der Nobelpreisträger Pjotr Leonidowitsch Kapiza, der die Suprafluidität bereits 1937 entdeckt hatte, bezeichnete dieses Helium II als "mehr als flüssig", denn es befindet sich in einem Quantenzustand, der sonst nur in Elementarteilchen vorkommt. Es vermag deshalb auch ungeachtet der Schwerkraft an Gefäßwänden hochzukriechen (!) oder, einmal angerührt, nahezu ewig zu wirbeln (!). Auch schlüpft es in Sekundenschnelle durch engste Kapillare hindurch, wozu gewöhnliches Helium Wochen benötigen würde.

Laut Kapiza strömt es widerstandslos. Wenn ein Gefäß mit superfluidem Helium allerdings in Drehung versetzt wird, dann macht die Flüssigkeit diese Bewegung nicht mit, sie bleibt einfach ruhig stehen. Dies gilt jedoch nur bei relativ langsamer Bewegung. Ab einer bestimmten Geschwindigkeit treten dann in der Flüssigkeit Wirbel auf. Dabei werden makroskopische Quanteneffekte wirksam. So wie die Bewegung eines einzelnen Elektrons um den Atomkern quantisiert ist, so ist in diesem Falle die kollektive Bewegung des aus zahllosen Atomen bestehenden Flüssigkeitswirbels quantisiert. Die Zirkulation kann daher nur bestimmte, durch das Plancksche Wirkungsquantum und die Masse des Heliumatoms gegebene Werte annehmen. ⁽⁴⁵⁾

Topologische Verformung des rotierenden Wassers

Topologische Verformung
des rotierenden Wassers

Doch dies ist ein besonderer Grenzfall, den ich auch nur erwähnt habe, um die Phantasie anzuregen und um zu belegen, daß es immer wieder überraschende Geschehnisse in der Natur gibt, von denen wir vor ihrer Entdeckung nicht das geringste geahnt hatten. Doch zurück zum Betrieb mit ,normalem’ Wasser.

Wenn Wasser in einem ruhenden Gefäß rotiert (mit einem Mixer kann man das leicht nachprüfen), dann steigt die Bremsenergie vom Mittelpunkt in Richtung Wandung, und bei Unterbrechung der Energiezufuhr zerfällt der Rotationsparaboloid auch sehr schnell wieder aufgrund der Wandreibung und der Scherkräfte.

Im Fall des sich drehenden Gefäßes haben diese Kräfte jedoch eine ganz andere Wirkung - vielmehr Funktion! -, denn wenn sich das Gefäß ebenfalls dreht, dann wird die Drehung zentripetal von der Wandung auf das Wasser im Innern übertragen. Hier bremst die Wandreibung also nicht, sondern ist ganz im Gegenteil sogar die Bedingung dafür, daß sich die Beschleunigung des Zylinders überhaupt auf das Wasser übertragen kann. Dieses Prinzip wird bei der Extraktions- und Dünnschichttechnik auch schon länger angewendet... z.B. mit Quecksilber. ⁽⁴⁶⁾

Beim Synergetischen Modell spielt noch ein weiterer Fakt eine sehr wesentliche Rolle: Das Wasser fließt hier ununterbrochen hindurch. Die Scherkräfte steigern sich von der Wandung zum Mittelpunkt hin jedoch nur während des Starts - und dies bei einem sich verringernden Durchmesser ebenfalls in schnell abnehmender Form.

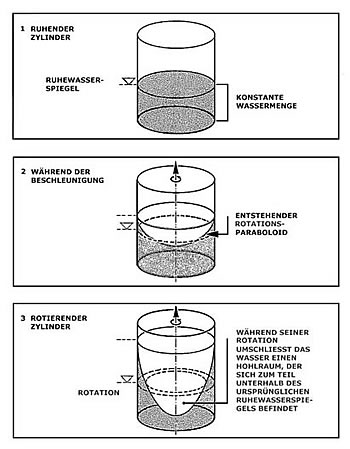
Doch betrachten wir erst einmal schrittweise was passiert, wenn ein Gefäß, das mit einer begrenzten Menge Wassers gefüllt ist und keinen offenen Wasserzufluß hat, in Rotation versetzt wird. Wie schon oben gesehen, verändert sich durch die Drehung die horizontale Oberfläche des ruhenden Wassers in einen Rotationsparaboloid. Die zweidimensionale Wasseroberfläche wird topologisch zu einer dreidimensionalen Fläche verformt. Ansonsten passiert aber nicht viel, da die Menge des Wassers ja begrenzt und unveränderlich ist (es sei denn, das Gefäß rotiert so schnell, daß das Wasser oben herausspritzt, aber so weit sind wir noch nicht...).

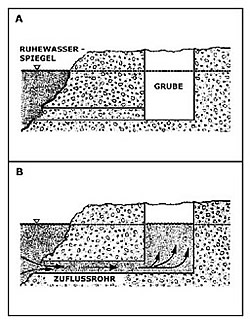
Baugrube mit Zuflußrohr

Ich möchte hier jedoch auf einen wesentlich Punkt hinweisen: Durch die Abdrängung des Wassers zur Seite - und damit nach oben - sinkt die Sohle des Rotationsparaboloids unterhalb des ursprünglichen Ruhewasserspiegels. In der Abbildung habe ich dieses Experiment mit einem rotierenden Zylinder verdeutlicht.

Bei dem rotierenden Kernmaschinenelement im Synergetischen Modell handelt sich ebenfalls um einen sich drehenden Zylinder - der allerdings unten eine zentrale Öffnung hat, durch die das Wasser stetig und ungehindert hineinfließen kann.

Dieser Zufluß erfolgt ohne jegliche Exergieaufwendung von unserer Seite - nämlich nach dem Prinzip der kommunizierenden Röhren. Dies wird dadurch erreicht, daß wir an Land eine Grube ausheben, deren Boden unterhalb des nahen Wasserspiegels liegt, und diese dann durch einen Zuflußkanal mit dem Wasserreservoir (Meer, See, Fluß ...) verbinden. Sobald man diesen Zufluß öffnet, wird sich die Grube bis zum Wasserspiegelniveau des Reservoirs mit Wasser füllen - von alleine. Auch dieses habe ich zur Verdeutlichung grafisch dargestellt.

Wenn der Rotationszylinder in dieser Grube nun so installiert wird, daß sich das untere Segment (Wassereinlaß, Schwungscheibe, Lagerung usw.) unterhalb des Null-Wasserspiegels befindet, dann geschieht folgendes:

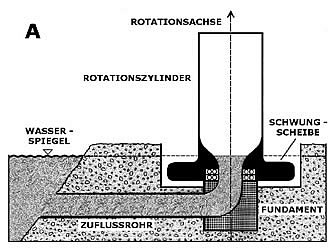
Funktion A - Ruhezustand

1. Das Wasser fließt durch das offene Zuflußrohr in den Rotationskörper hinein und kommt - solange sich dieser noch in Ruhe befindet - auf dem Null-Wasserspiegelniveau zur Ruhe. In den folgenden Grafiken stelle ich die einzelnen Etappen dar, wobei (A) die Situation vor dem Beginn der Beschleunigung beschreibt.

2. Da der Rotationskörper des Synergetischen Modells von einem ständigen Wassernachfluß jedoch nicht abgeschnitten ist, bildet sich während des Starts ein Rotationsparaboloid heraus, ohne daß aber dabei ein Hohlraum unterhalb des Null-Niveaus entstehen kann - da dieser ja sofort wieder von nachdrängendem Zuflußwasser ausgefüllt wird. Die Versorgung mit Zuflußwasser funktioniert also alleine durch diesen architektonischen ,Trick’ und bedarf tatsächlich keiner weiteren Exergieaufwendung unsererseits. Nun wird auch die Wichtigkeit der geophysikalischen Koordinaten klar, mit denen ich dieses Kapitel begonnen habe.

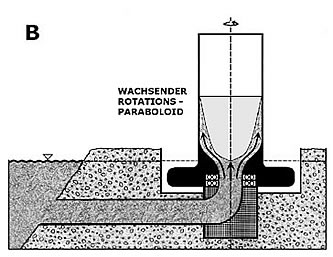
Funktion B - Start

3. Während der anlaufenden Beschleunigungsperiode ,füllt’ sich der Rotationskörper nicht nur mit mechanischer Energie, sondern auch mit ständig nachfließendem Wasser (B). Je länger die Beschleunigungsphase anhält, desto höher steigt das rotierende Wasser - und zwar solange, bis es den oberen Rand des Rotationskörpers erreicht und aus ihm herausgeschleudert wird (C).

4. Das Niveau des Speisewasserspiegels ist theoretisch der konstante Tiefstpunkt des entstandenen Rotationsparaboloids. In der Praxis wird sich durch den offenen Nachfluß allerdings herausstellen, daß sich der Rotationswirbel innerhalb des Zylinders auch unterhalb des Null-Niveaus und - sofern dies nicht unterbunden wird - sogar durch das Zuflußrohr bis in das Wasserreservoir hinein fortsetzen wird. Auf diese und andere Strömungen sowie auf die Möglichkeiten ihrer Ausnutzung werde ich noch zurückkommen.

Im Laufe der beschriebenen Etappen bewirkt der offene Zufluß in das Rotationsmaschinenelement die Speicherung des einfließenden Wassers und damit eine Gewichtszunahme der rotierenden Gesamtmasse, womit wiederum eine höhere Speicherfähigkeit für mechanische Energie erreicht wird. Dies geschieht so lange, bis das sich hinaufdrehende Wasser den oberen Rand des Rotationsmaschinenelements erreicht und über diesen hinweg herausgeschleudert wird. Das Wasser hat damit den Zylinder von unten nach oben durchflossen.

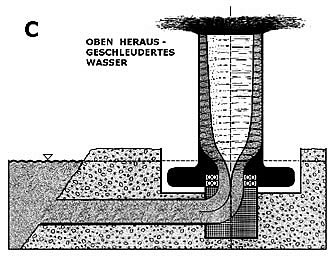
Funktion C - In Betrieb

Die Möglichkeit dieses ,Durchfließens’ ist natürlich von der Funktion abhängig, daß das Wasser oben auch wieder hinausfließen kann. Dieser konstante Durchfluß erfordert eine konstante Drehzahl, stabilisiert damit das Gesamtgewicht, und hilft damit wiederum, die Rotationsgeschwindigkeit zu stabilisieren. Hier erkennen wir bereits einige der einfachen Wechselwirkungseffekte im makroskopischen Bereich - in Form eines mehrfachen Regelkreises von einander beeinflussenden physikalischen Geschehnissen. Im Resultat erzielen wir dadurch das gewünschte Fließgleichgewicht, auf das ich nun im Detail eingehen werde.

Eine Planskizze der kompletten Anlage mitsamt Wasserauffangbecken, Fallschacht, Turbine usw. befindet sich am Ende dieses Teiles.

Weiter...