Buch der Synergie

 TEIL D
TEIL D
OPTIMIERUNG
Ich möchte die variablen
Parameter, die es zu optimieren gilt, in zwei Gruppen unterteilen - die
Konstruktionsparameter und die Betriebsparameter.
Um die optimale Form des Rotationsmaschinenelements zu finden (ich sage hier bewußt nicht Rotationszylinder), kommen wir nicht umhin, Versuche und Experimente durchzuführen, wobei allerdings auch die Möglichkeit besteht, mit Simulationstechniken wie der Evolutionsstrategie zu arbeiten.
Es gibt allerdings schon einige Ausgangspunkte, von denen aus dieser Weg beschritten werden kann. So läßt sich bereits an einem kleinen Modell aufzeigen, wie positiv sich die Schwungscheibenmasse auf die Speicherung kinetischer Energie auswirkt - und damit auch auf die Steigerung der dynamischen Masse.
Die Konstruktionsparameter
1 - Masse
Die ,Ruhemasse’ des Rotationszylinders sollte möglichst
groß sein.
Dem gegenwärtigen Stand der Technik entsprechend sind Schwungscheiben
zur Steigerung der Ruhemasse am vorteilhaftesten. In Teil C steht unter
,Energiespeicherung’ mehr über die verschiedenen, bereits angewandten Schwungmassen-Technologien.
Die anteilige Wirkung der Masse auf das Verhalten des Gesamtsystems kann aber erst anhand variabler Versuchsmodelle und meßbarer Pilotanlagen bestimmt werden. Nichtsdestotrotz handelt es sich bei der Aussage ,möglichst schwer’ um eine des ursprünglichen ,Innovators’ des Synergetischen Modells, der diese auch wieder und wieder betont hat. Habe ich es mir nur eingebildet, oder war die rotierende Wasserwand in den Kleinmodellen tatsächlich auch dicker, wenn der Eimer eine schwerere Schwungscheibe hatte?! (204)
2 - Maße
Hier ist neben
der gewünschten bzw. erforderlichen Höhe auch ein entsprechend großer
Durchmesser des Rotationszylinders zu berücksichtigen.
Ein Grund hierfür ist
die Tatsache, daß das Trägheitsmoment mit zunehmender Entfernung
der Masse von der Drehachse ebenfalls zunimmt. Zugunsten eines optimalen
Durchflusses ist außerdem ein Zufluß mit möglichst
großem Durchmesser wichtig.
Die Minimaldrehzahl ergibt sich rechnerisch aus der Relation zwischen Höhe und Durchmesser des Rotationszylinders. Hohe und dünne Rohre würden also extrem hohe Drehzahlen erfordern - während breite und flache Schalen schon nach wenigen langsamen Drehungen überschwappen. Intuitiv gehe ich daher von ,ästhetischen Relationen’ aus - und stelle mir einen großen rotierenden Zylinder vor, stählern, oder auch aus Plexiglas... mächtiger als ein Gastank, aber nicht so gewaltig wie ein Kühlturm. Dazu paßt auch sehr gut, daß in der Hydroelektrik gerne mit Fallhöhen über 20 m gearbeitet wird (205).
3 - Form
Auch hier wird
vermutlich der Versuch das beste Resultat erbringen,
es liegt aber nahe, die Form des Rotationsmaschinenelements entsprechend
der topologischen Verformung des Wassers während der Rotation
auszulegen. Prof. Trostel war der erste, der außerdem für
einen winkelfreien, kelchförmigen und strömungsdynamischen
Einfluß plädierte.
Ich bin mir ziemlich sicher, daß die optimale Form des Rotationsmaschinenelements die eines Rotationszylinders ist. Ein Indiz dafür ist die Tatsache, daß zumindest Schüttel-Strömungen schnell zum Erliegen kommen, wenn die Wandung zu glatt ist - oder wenn die Gefäßwände schräg sind! (206)
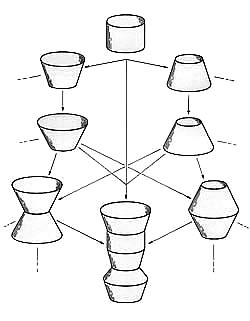
Aber warum nicht auch mit anderen Formen experimentieren? Ich schlage daher vor, ausgehend vom Hohlzylinder, diesen selbst sowie verschiedene Hohlkegelsegmente mit verschiedenen Winkelgraden miteinander zu kombinieren. Die Kombinationen mit den besten Ergebnissen können anschließend strömungsdynamisch weiter optimiert werden. In der Abbildung habe ich den Anfang einer derartigen Testreihe dargestellt. Nach den ersten realen Modellen kann diese Reihe über weite Strecken durch evolutionsstrategische Algorithmen simuliert werden.
4 - Material
Die
Materialoptimierung hängt von der chemischen Zusammensetzung der
Durchflußsubstanz ab (Meerwasser ist bekanntermaßen besonders
aggressiv), von dem möglicherweise verstärkbaren und damit
auch verstärkt nutzbaren
thermischen Austausch zwischen Durchflußsubstanz
und Material, sowie von der Oberflächenbeschaffenheit der Innenseite
des Rotationszylinders.
Sollten außerdem noch magnetische und/oder elektrische Felder eine Rolle spielen - und das tun sie ziemlich sicher -, dann wird das Herausfinden der passenden Legierungen sicherlich noch viel Spaß machen, obwohl ich mir genauso gut vorstellen kann, daß sich völlig passive Elemente als besonders sinnvoll erweisen werden. Die Materialoptimierung ist auf jeden Fall ein Bereich, der besonders viele Versuche erfordert.
Den Optimierungskriterien der Oberfläche werden wohl am ehesten Edelmetall-Legierungen und metallischen Gläsern entsprechen, denn neben der Korrosionsbeständigkeit gelten als wichtige Parameter auch die allgemeine Verschleißfestigkeit sowie die Härte und die Zähigkeit des Materials. Sicherlich gibt es noch viele weitere Alternativen... und möglicherweise sogar Felder, die die ,grobstoffliche’ Materie völlig ersetzen.
Die Betriebsparameter
Diese
beschränken sich auf die Steuerung von Rotationsgeschwindigkeit
und Durchflußmenge. Während die Durchflußmenge im
Sinne der Gesamtkapazität des Synergetischen
Modells möglichst groß
sein soll, sollte die Rotationsgeschwindigkeit dagegen möglichst
niedrig liegen. Eine stabile Drehzahl läßt
sich dabei durch das Antriebs-, Kontroll- und Bremssystem erreichen
und aussteuern.
Wenn die oft postulierte Selbstverstärkung des Wirbels nun auch im Rotationszylinder geschieht, dann gewinnt damit auch die Aussage des ,Innovators’ Al-Khooss neues Gewicht, "daß der Rotationskörper unbedingt mit Bremsen versehen werden muß". Denn eine zu hohe Drehzahl würde vermutlich (neben der Gefahr der Materialzerstörung) zu einem Zerreißen des Molekularverbandes des hinauffließenden Wassers führen und die Förderung unterbrechen.
Andererseits bildet die Instabilität ein wesentliches Element synergetischer Prozesse: "Die Instabilität ist die Voraussetzung für Selbstorganisation. (...) Eben dies müßte man einbeziehen in so etwas wie technische Entwurfsprozesse" (207).
Nun - genau daran soll hier ja gearbeitet werden...!
Einen weiteren Parameter bildet die Relation zwischen -h und +h innerhalb der geophysikalischen Koordinaten (s.o.), welche entweder unveränderbar zu den Konstruktions-, oder veränderbar zu den Betriebsparametern gehören kann. Im letzteren Fall würde eine Hydraulik das System einige Dezimeter anheben oder absenken, um damit die Stärke des Druckes zu verändern, der sich durch das Zuflußwasser in das System hinein fortsetzt.
Das abschließende Kapitel dieses Teiles beschäftigt sich mit allgemeinen Überlegungen zu Anwendungen und Nebeneffekten des Synergetischen
Modells.